


Next: About this document ...
documentclass[a4paper]article
par
usepackagea4wide
usepackagetimes
par
usepackage[ngerman]babel
usepackage[isolatin]inputenc
usepackagemulticol
usepackageamsmath,amssymb
usepackagewasysym
par
newedcommandRmathbbR
newedcommandZmathbbZ
newedcommandequivalentLeftrightarrow
newedcommandabs[1]left|#1right|
par
newedcommandquantexpr[2]
beginmultline*
#1
#2
endmultline*
par
begindocument
par
titleQuantorenmechanik
authorHenning Thielemann
maketitle
par
abstract
Dieser Artikel befasst sich mit der weit verbreiteten Gewohnheit,
Allquantoren hinter die quantifizierten Aussagen zu schreiben.
Diese Schreibweise ist allerdings inkonsistent und
mitunter auch missverständlich.
par
beginmulticols2
par
sectionProblem
par
Um zu demonstrieren, worum es geht,
nehmen wir einmal die allseits bekannte Definition
für die Stetigkeit einer reellen Funktion
über ihrem gesamten Definitionsbereich her
und lassen diese Formel einfach auf uns wirken:
quantexpr
forall varepsilon > 0 : exists delta > 0 : forall y in R :
absx-y < delta implies absf(x)-f(y) < varepsilon qquadforall x in R
par
So könnte dieser Ausdruck an der Tafel in einer beliebigen
AnalysisI-Vorlesung gestanden haben.
par
Huh, da fängt aber unser hochverehrter textscGeorg Quantor
im Grabe an zu rotieren.
Deshalb Halt, liebe Kinder zu Hause an den Bildschirmen,
macht das nicht nach!
Bitte schreibt das nicht ab und behauptet,
Ihr hättet es von mir!
Denn was da steht, ist Murks.
par
textitWas hat er denn nur?
par
Überlegt genau, was da wirklich steht! Steht da
quantexpr
forall x in R : forall varepsilon > 0 :
exists delta > 0 : forall y in R :
absx-y < delta implies absf(x)-f(y) < varepsilon
was der normalen Stetigkeit entspricht, oder soll es
quantexpr
forall varepsilon > 0 : exists delta > 0 :
forall x in R : forall y in R :
absx-y < delta implies absf(x)-f(y) < varepsilon
bedeuten, was der gleichmäßigen Stetigkeit entspricht?
par
glqqJagrqq, sagt der versierte Quantoren-Anwender,
glqqworauf sich die Quantoren beziehen,
das ersieht man doch aus dem Kontext.grqq
Diese gerne hervorgebrachte Widerrede
haben wir mit diesem Fall so eben elegant ausgehebelt.
Hm, was ist eigentlich dagegen einzuwenden,
wenn man der uneindeutigen Variante die eindeutige vorzieht,
ohne dabei mehr schreiben zu müssen?
par
Ich habe sogar schon gesehen,
dass
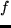 geschrieben wird,
um zu verdeutlichen, dass bei der gleichmäßigen Stetigkeit
das
geschrieben wird,
um zu verdeutlichen, dass bei der gleichmäßigen Stetigkeit
das  nicht vom
nicht vom 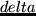 abhängt. -
Schauderhaft, nicht wahr?
par
Jedoch sollte man die Diskussion gar nicht anhand der Eindeutigkeit führen,
denn natürlich gibt es häufig Fälle in denen auch falsch gesetzte Quantoren
irgendwie glqqeindeutiggrqq interpretiert werden können.
par
Ein Blick auf die Ursprünge der Quantoren soll helfen,
sie besser zu verstehen:
par
sectionWoher kommen die Quantoren?
par
Na das ist doch ganz klar:
Quantoren sind symbolische Abkürzungen für die Redewendungen
glqqfür allegrqq und glqqes gibt mindestens eingrqq.
Das weiß doch jeder Erstsemestler.
Leider.
Nur weil es hinreichend viele Professoren so sehen,
ist es aber noch nicht richtig.
par
Wie ist es denn nun richtig?
par
Fangen wir ganz von vorne an.
Im Folgenden soll die Zahl
abhängt. -
Schauderhaft, nicht wahr?
par
Jedoch sollte man die Diskussion gar nicht anhand der Eindeutigkeit führen,
denn natürlich gibt es häufig Fälle in denen auch falsch gesetzte Quantoren
irgendwie glqqeindeutiggrqq interpretiert werden können.
par
Ein Blick auf die Ursprünge der Quantoren soll helfen,
sie besser zu verstehen:
par
sectionWoher kommen die Quantoren?
par
Na das ist doch ganz klar:
Quantoren sind symbolische Abkürzungen für die Redewendungen
glqqfür allegrqq und glqqes gibt mindestens eingrqq.
Das weiß doch jeder Erstsemestler.
Leider.
Nur weil es hinreichend viele Professoren so sehen,
ist es aber noch nicht richtig.
par
Wie ist es denn nun richtig?
par
Fangen wir ganz von vorne an.
Im Folgenden soll die Zahl 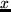 immer eine ganze Zahl bezeichnen.
Nehmen wir als Beispiel die Aussage
beginquote
immer eine ganze Zahl bezeichnen.
Nehmen wir als Beispiel die Aussage
beginquote
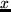 ist eine gerade Zahl.
endquote
oder kurz
beginquote
ist eine gerade Zahl.
endquote
oder kurz
beginquote
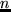 endquote
Behaupten kann man es einfach einmal.
Hm, für
endquote
Behaupten kann man es einfach einmal.
Hm, für 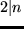 und
und 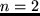 zum Beispiel stimmt die Aussage sogar.
par
beginquote
zum Beispiel stimmt die Aussage sogar.
par
beginquote
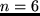 endquote
par
beginquote
textttType mismatch in line 1:
endquote
par
beginquote
textttType mismatch in line 1:
texttt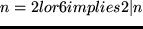 requires boolean as operands
endquote
par
Ich wollte Euch doch nur mal testen. Obwohl sich
beginquote
Wenn
requires boolean as operands
endquote
par
Ich wollte Euch doch nur mal testen. Obwohl sich
beginquote
Wenn 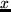 gleich
gleich 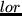 oder
oder 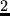 ist,
ist,
dann ist 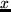 eine gerade Zahl.
endquote
ganz vernünftig anhört, ist die 1:1-Übersetzung in Symbole völlig daneben.
Richtig ist selbstverständlich:
beginquote
eine gerade Zahl.
endquote
ganz vernünftig anhört, ist die 1:1-Übersetzung in Symbole völlig daneben.
Richtig ist selbstverständlich:
beginquote
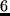 endquote
par
Aber es gibt noch viel mehr gerade Zahlen.
begineqnarray*
&&(n = 0 implies 2|n) land
endquote
par
Aber es gibt noch viel mehr gerade Zahlen.
begineqnarray*
&&(n = 0 implies 2|n) land
&&(n = -2 implies 2|n) land (n = 2 implies 2|n)land
&&(n = -4 implies 2|n) land (n = 4 implies 2|n) dots
endeqnarray*
Hm, glqqdotsgrqq ist aber nicht besonders exakt.
par
Ob man vielleicht das Und-Symbol wie ein Summenzeichen verwenden kann?
par
par
Aber kann man das so hinschreiben?
Ja, man kann.
Man trifft diese Notation zwar nur selten an,
aber sie ist richtig.
Diesen Ausdruck kann man jetzt auch lesen als
beginquote
Für alle 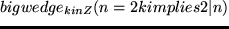 gilt:
gilt:
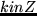 .
endquote
par
Die gebündelte Schreibweise hat gegenüber glqqdotsgrqq
zudem den Vorteil,
dass man auch über überabzählbare Mengen etwas aussagen kann.
par
Nun kann man statt
.
endquote
par
Die gebündelte Schreibweise hat gegenüber glqqdotsgrqq
zudem den Vorteil,
dass man auch über überabzählbare Mengen etwas aussagen kann.
par
Nun kann man statt 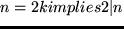 auch ein
auch ein 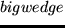 schreiben,
die Laufvariable statt darunter daneben setzen und
den Implikationspfeil zum Doppelpunkt machen,
und man erhält die gleiche Aussage, nur anders aufgeschrieben.
Wie Ihr seht,
hat die der menschlichen Sprache nähere Symbolik mit
schreiben,
die Laufvariable statt darunter daneben setzen und
den Implikationspfeil zum Doppelpunkt machen,
und man erhält die gleiche Aussage, nur anders aufgeschrieben.
Wie Ihr seht,
hat die der menschlichen Sprache nähere Symbolik mit 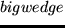 die Oberhand gewonnen,
und diese hat dann wohl den heutigen Missverständnissen den Weg geebnet.
Bei
die Oberhand gewonnen,
und diese hat dann wohl den heutigen Missverständnissen den Weg geebnet.
Bei 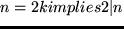 käme vermutlich keiner auf die Idee,
es hinter den quantifizierten Ausdruck zu schreiben,
genauso wie es sich keiner wagt,
zu schreiben, wenn er die ganzen Zahlen von 0 bis
käme vermutlich keiner auf die Idee,
es hinter den quantifizierten Ausdruck zu schreiben,
genauso wie es sich keiner wagt,
zu schreiben, wenn er die ganzen Zahlen von 0 bis 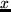 addieren will.
Wenn man schon unbedingt etwas
hinter einen zu quantifizierenden Ausdruck schreiben will,
dann bitte Verbales wie glqqfür alle
addieren will.
Wenn man schon unbedingt etwas
hinter einen zu quantifizierenden Ausdruck schreiben will,
dann bitte Verbales wie glqqfür alle  grqq
oder glqqfür ein
grqq
oder glqqfür ein 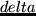 grqq.
par
Analog zu
grqq.
par
Analog zu 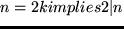 kann man auch die Aussage
beginquote
Es gibt ungerade Zahlen.
endquote
in Symbole fassen.
kann man auch die Aussage
beginquote
Es gibt ungerade Zahlen.
endquote
in Symbole fassen.
par
kurz
par
par
Wenn man sich als Eselsbrücke merkt,
dass 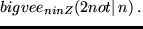 ein Element,
für das die Aussage zutrifft, aufspießt,
während
ein Element,
für das die Aussage zutrifft, aufspießt,
während 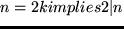 an der Unterseite viel Platz
für alle Elemente bietet, auf die die Aussage zutrifft,
ist die Verwendung dieser beiden Symbole
mindestens genauso intuitiv wie
an der Unterseite viel Platz
für alle Elemente bietet, auf die die Aussage zutrifft,
ist die Verwendung dieser beiden Symbole
mindestens genauso intuitiv wie 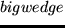 und
und 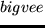 .
par
sectionFolgerungen
par
Mit diesem Hintergrundwissen ausgestattet wundert es einen
nicht mehr, dass das Negieren einer quantifizierten Aussage etwas mit dem
textscde Morganschen Gesetz zu tun hat. Zur Erinnerung:
beginalign*
intertextOriginal:
neg (a lor b) &equivalent neg a land neg b
.
par
sectionFolgerungen
par
Mit diesem Hintergrundwissen ausgestattet wundert es einen
nicht mehr, dass das Negieren einer quantifizierten Aussage etwas mit dem
textscde Morganschen Gesetz zu tun hat. Zur Erinnerung:
beginalign*
intertextOriginal:
neg (a lor b) &equivalent neg a land neg b
neg (a land b) &equivalent neg a lor neg b
intertextVerallgemeinert:
neg bigvee_x A(x) &equivalent bigwedge_x neg A(x)
neg bigwedge_x A(x) &equivalent bigvee_x neg A(x)
endalign*
Während man an einer korrekt aufgedröselten Negation der verbalen
Formulierung der Stetigkeit (und an der Variante mit bunt durcheinander
gewürfelten Quantoren erst recht) ganz schön zu knabbern hat, kann man das
Gleiche bei korrekter Notation problemlos völlig mechanisch abwickeln.
Danach ist eine reelle Funktion genau dann nicht überall stetig, wenn:
quantexpr
exists x in R : exists varepsilon > 0 : forall delta > 0 : exists y in R :
absx-y < delta land absf(x)-f(y) ge varepsilon
par
sectionZusammenfassung
par
Wir haben gesehen, dass Quantoren eine exakte Interpretation in der Logik haben.
Sie sind Rechensymbole und unterliegen daher einer festen Syntax.
Man kann nun eine Diskussion vom Zaun brechen,
welche Syntax sinnvoll ist und welche nicht.
Aus Konsistenzgründen (siehe Summenzeichen)
ist die Schreibweise mit vorangestellten Quantoren vorzuziehen.
par
sectionAusblick
par
Gerade in einer Zeit,
in der Computerprogramme zum automatischen Lösen und
Beweisen mathematischer Problemstellungen den Markt erobern,
ist eine korrekte Notation absolut notwendig.
Macht man sich keine Gedanken über die Sachen, die man aufschreibt,
oder jene, die man der Einfachheit halber weglässt,
kann einem auch das beste Computeralgebra-System nicht weiterhelfen.
Diese Systeme sind überhaupt erst
durch eine konsequente Formalisierung der Mathematik möglich geworden
und sollten Rechtfertigung genug sein
für das oft misstrauisch beäugte Bemühen der Mathematiker,
ihre Wissenschaft zu formalisieren.
par
Alle Studenten, die sich bis jetzt nicht getraut haben,
Ihre Professoren darauf hinzuweisen,
dürfen nun diesen Artikel schwarz auf weiß ihren
Vorlesenden unter die Nasen reiben, hehe.
Oder um es einmal so zu formulieren:
par
begineqnarray*
M &:& textMenge aller Studenten
A(x) &:& x textbislang nicht mutig genug
B(x) &:& x texthat diesen Artikel gelesen
C(x) &:& x textdarf Professor diesen Artikel
& & textunter die Nase reiben
endeqnarray*
par
endmulticols
enddocument



Next: About this document ...
Henning Thielemann
2004-06-25